Model category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms ('arrows') called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes (derived category theory). This concept was introduced by Daniel G. Quillen (1967).
Contents |
Motivation
Model categories can provide a natural setting for homotopy theory: the category of topological spaces is a model category, with the homotopy corresponding to the usual theory. Similarly, objects that are thought of as spaces often admit a model category structure, such as the category of simplicial sets.
Another model category is the category of chain complexes of R-modules for a commutative ring R. Homotopy theory in this context is homological algebra. Homology can then be viewed as a type of homotopy, allowing generalizations of homology to other objects, such as groups and R-algebras, one of the first major applications of the theory. Because of the above example regarding homology, the study of closed model categories is sometimes thought of as homotopical algebra.
Formal definition
The definition given initially by Quillen was that of a closed model category, the assumptions of which seemed strong at the time, motivating others to weaken some of the assumptions to define a model category. In practice the distinction has not proven significant and most recent authors work with closed model categories and simply drop the adjective 'closed'.
The definition has been separated to that of a model structure on a category and then further categorical conditions on that category, the necessity of which may seem unmotivated at first but becomes important later. The following definition follows that given by Hovey.
A model structure on a category C consists of three distinguished classes of morphisms (equivalently subcategories): weak equivalences, fibrations, and cofibrations, and two functorial factorizations 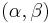 and
and 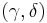 subject to the following axioms. Note that a fibration that is also a weak equivalence is called an acyclic (or trivial) fibration and a cofibration that is also a weak equivalence is called an acyclic (or trivial) cofibration (or sometimes called an anodyne morphism). (Some readers find the term "trivial" ambiguous and so prefer to use "acyclic".)
subject to the following axioms. Note that a fibration that is also a weak equivalence is called an acyclic (or trivial) fibration and a cofibration that is also a weak equivalence is called an acyclic (or trivial) cofibration (or sometimes called an anodyne morphism). (Some readers find the term "trivial" ambiguous and so prefer to use "acyclic".)
- Axioms
- Retracts: if g is a morphism belonging to one of the distinguished classes, and f is a retract of g (as objects in the arrow category
 , where 2 is the 2-element ordered set), then f belongs to the same distinguished class. Explicitly, the requirement that f is a retract of g means that there exist i, j, r, and s, such that the following diagram commutes:
, where 2 is the 2-element ordered set), then f belongs to the same distinguished class. Explicitly, the requirement that f is a retract of g means that there exist i, j, r, and s, such that the following diagram commutes: - 2 of 3: if f and g are maps in C such that f, g, and gf are defined and any two of these are weak equivalences then so is the third.
- Lifting: acyclic cofibrations have the left lifting property with respect to fibrations and cofibrations have the left lifting property with respect to acyclic fibrations. Explicitly, if the outer square of the following diagram commutes, where i is a cofibration and p is a fibration, and i or p is acyclic, then there exists h completing the diagram.
- Factorization:
- every morphism f in C, can be written as
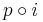 for a fibration p and an acyclic cofibration i;
for a fibration p and an acyclic cofibration i; - every morphism f in C, can be written as
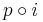 for an acyclic fibration p and a cofibration i.
for an acyclic fibration p and a cofibration i.
- every morphism f in C, can be written as
A model category is a category that has a model structure and all (small) limits and colimits, i.e. a complete and cocomplete category with a model structure.
Examples
The category of topological spaces, Top, admits a standard model category structure with the usual (Serre) fibrations and cofibrations and with weak equivalences as weak homotopy equivalences. This structure is not unique; in general there can be many model category structures on a given category. For the category of topological spaces, another such structure is given by Hurewicz fibrations and cofibrations.
The category of (nonnegatively graded) chain complexes of R-modules carries at least two model structures, which both feature prominently in homological algebra:
- weak equivalences are maps that induce isomorphisms in homology;
- cofibrations are maps that are monomorphisms in each degree with projective cokernel; and
- fibrations are maps that are epimorphisms in each nonzero degree
or
- weak equivalences are maps that induce isomorphisms in homology;
- fibrations are maps that are epimorphisms in each degree with injective kernel; and
- cofibrations are maps that are monomorphisms in each nonzero degree.
This explains why Ext-groups of R-modules can be computed by either resolving the source projectively or the target injectively. These are cofibrant or fibrant replacements in the respective model structures.
The category of arbitrary chain-complexes of R-modules has a model structure that is defined by
- weak equivalences are chain homotopy equivalences of chain-complexes;
- cofibrations are monomorphisms that are split as morphisms of underlying R-modules; and
- fibrations are epimorphisms that are split as morphisms of underlying R-modules.
Other examples of categories admitting model structures include the category of all small categories, the category of simplicial sets or simplicial presheaves on any small Grothendieck site, the category of topological spectra, and the categories of simplicial spectra or presheaves of simplicial spectra on a small Grothendieck site.
Simplicial objects in a category are a frequent source of model categories; for instance, simplicial commutative rings or simplicial R-modules admit natural model structures. This follows because there is an adjunction between simplicial sets and simplicial commutative rings (given by the forgetful and free functors), and in nice cases one can lift model structures under an adjunction.
Denis-Charles Cisinski has developed[1] a general theory of model structures on presheaf categories (generalizing simplicial sets, which are presheaves on the simplex category).
Some constructions
Every closed model category has a terminal object by completeness and an initial object by cocompleteness, since these objects are the limit and colimit, respectively, of the empty diagram. Given an object X in the model category, if the unique map from the initial object to X is a cofibration, then X is said to be cofibrant. Analogously, if the unique map from X to the terminal object is a fibration then X is said to be fibrant.
If Z and X are objects of a model category such that Z is cofibrant and there is a weak equivalence from Z to X then Z is said to be a cofibrant replacement for X. Similarly, if Z is fibrant and there is a weak equivalence from X to Z then Z is said to be a fibrant replacement for X. In general, not all objects are fibrant or cofibrant, though this is sometimes the case. For example, all objects are cofibrant in the standard model category of simplicial sets and all objects are fibrant for the standard model category structure given above for topological spaces.
Left homotopy is defined with respect to cylinder objects and right homotopy is defined with respect to path objects. These notions coincide when the domain is cofibrant and the codomain is fibrant. In that case, homotopy defines an equivalence relation on the hom sets in the model category giving rise to homotopy classes.
Characterizations of fibrations and cofibrations by lifting properties
Cofibrations can be characterized as the maps which have the left lifting property with respect to acyclic fibrations, and acyclic cofibrations are characterized as the maps which have the left lifting property with respect to fibrations. Similarly, fibrations can be characterized as the maps which have the right lifting property with respect to acyclic cofibrations, and acyclic fibrations are characterized as the maps which have the rightlifting property with respect to cofibrations.
Homotopy and the homotopy category
Given a model category, one can then define an associated homotopy category by localizing with respect to the class of weak equivalences. This suggests that the information regarding homotopy is contained in the class of weak equivalences whereas the classes of fibrations and cofibrations are useful in making constructions within the category. For example, the homotopy category for the model category structure on topological spaces given above is the category of CW-complexes. This is also true for the model category of simplicial sets. Simplicial sets have nice combinatorial properties and are often used as models for topological spaces because of the equivalence of the homotopy categories.
References
- D.-C. Cisinski: Les préfaisceaux commes modèles des types d'homotopie, Astérisque, (308) 2006, xxiv+392 pp.
- W. G. Dwyer and J. Spalinski: Homotopy Theories and model categories, 1995. [1]
- Philip S. Hirschhorn: Model Categories and Their Localizations, 2003, ISBN 0-8218-3279-4.
- Mark Hovey: Model Categories, 1999, ISBN 0-8218-1359-5.
- K. H. Kamps and T. Porter: Abstract homotopy and simple homotopy theory, 1997, World Scientific, ISBN 981-02-1602-5.
- G. Maltsiniotis: La théorie de l'homotopie de Grothendieck. Astérisque, (301) 2005, vi+140 pp.
- Quillen, Daniel G. (1967), Homotopical algebra, Lecture Notes in Mathematics, No. 43, 43, Berlin, New York: Springer-Verlag, doi:10.1007/BFb0097438, MR0223432
External links
- Model category in ncatlab
- Model category in Joyal's catlab
- ^ Cisinski, Denis-Charles. Les préfaisceaux comme modèles des types d'homotopie. (French) [Presheaves as models for homotopy types] Astérisque No. 308 (2006), xxiv+390 pp. ISBN 978-2-85629-225-9 MR2294028